DISTANCIA Y TAMAÑO DE LA LUNA

Miguel Gilarte

Las antiguas civilizaciones orientales, persas, egipcias, árabes, griegas o romanas, nos han dejado un legado de suma importancia para nuestros días. Ellos fueron los precursores de la Astronomía moderna. Comenzaron a etiquetar los planetas y estrellas bajo un mismo nombre común a todos los observadores del planeta Tierra y poder arrancar de esta manera de una incipiente salida que les catapultara con el tiempo a los confines del Universo.

Gracias a ellos conocemos hoy día datos de gran valía, que nos han ayudado a esclarecer dudas de ciertos acontecimientos. Por ejemplo el paso de cometas como el Halley, registrado en todos sus acercamientos a la Tierra desde el año 239 a.d.c. o de las apariciones de explosiones de estrellas a las que llamaban novas o estrellas huéspedes, que nos han servido de punto de referencia para orientar hoy día los telescopios y visualizar los restos de las mismas que forman nebulosas planetarias; tal es el caso de la nebulosa del Cangrejo (MI ) en la constelación de Tauro, de la que hoy contemplamos los restos de una explosión estelar, contemplada por los chinos en el año 1.054 de nuestra era. En el libro "Historia de la Dinastía Sung ", leemos:

"Primer año del reinado de Chi-Ho, 5º mes, día de Chi-Chian. Una estrella huésped apareció varias pulgadas al sureste de TienKuan. Algo más de un año después desapareció poco a poco.”

Estos datos corresponden a la fecha de 4 de Julio del año 1.054 después de Cristo. La estrella referida "TienKunes” es ahora S Tauri. A una distancia más o menos de medio grado de esta.

La civilización griega nos informó de otros acontecimientos quizás aun más desconcertantes para aquella lejana época. Nos mostraron de forma fácil el camino a seguir hasta el descubrimiento del tamaño de la Tierra, para luego medir por primera vez en la historia, la distancia y diámetro de un cuerpo extraterrestre: la Luna.

El hombre de aquel tiempo llegó a la certeza de que la tierra debería ser redonda. Dos datos empíricos nos conducen a ello:

1.     Los barcos vistos desde la costa, no desaparecían poco a poco en la distancia (lo que confirmaría una Tierra plana), sino que antes dejaba de ser visible la proa y luego la popa, como si la embarcación descendiera sobre una pendiente o cayera a un agujero, pero esto no ocurría pues la embarcación regresaba a puerto. La explicación, debiera estar en que la Tierra es redonda.

2.     Otro dato que lo confirmaba, fue el hecho que cuando tenía lugar un eclipse de Luna, la sombra que la Tierra proyectaba sobre nuestro satélite, era circular y no una línea en caso de que fuese plana.

Conocer el diámetro de la Tierra no fue ardua tarea según los conocimientos que poseían los geógrafos griegos. Los primeros trabajos para el conocimiento del perímetro de la Tierra, los puso en práctica .Eratóstenes de Cirene (276 a 196 a.C.), conocido filósofo griego que además fue un notable de la Astronomía y geografía, llegando a ser director de la colosal Biblioteca de Alejandría en la corte de Ptolomeo III.

El 21 de Junio, el Sol pasaba justamente por el meridiano y cénit de la ciudad egipcia de Syene (ahora Assuan). Si nosotros clavamos en el suelo de esta ciudad un objeto, como bien pueda ser un tocho, vertical, comprobaremos que no proyecta sombra alguna (durante el tiempo que el Sol permanece en el cénit), pero en otra ciudad escogida para tal experimento, que resultó ser Alejandría a 800 Km. de distancia, se colocó verticalmente otro tocho, que sí proyectaba sombra, pues en aquel lugar no incidía el Sol desde el cénit, sino desde una perspectiva inclinada de 7º. Así pues, la sombra que el tocho proyectaba, también era de 7º.

Los resultados fueron sorprendentes. Con ello se demostraba que la Tierra es redonda, pero lo más interesante fue: si 7º equivalen a 800 Km. (distancia entre los dos puntos de referencia), 360º equivaldrían a 41.143 Km., o bien 252.000 estadios en unidades de la época. Esta se convirtió en la longitud de la circunferencia estimada para el planeta Tierra. Hoy se calcula en 39.921 Km.

Con estos importantísimos datos, el hombre podía dar un gran salto de la Tierra a la Luna y medir algunos parámetros de éste., basados en su madre la Tierra.

Un notable astrónomo griego (320 a 250 a.C.) llamado Aristarco de Samos, fue el primero en darnos unos resultados sobre la distancia de la Tierra y el Sol; aunque no estuvo muy acertado en sus cálculos. Por ejemplo estimó que el Sol debía medir siete diámetros terrestres y tener un volumen trescientas veces mayor que nuestro planeta. Como se puede apreciar, se quedó muy corto en sus cuentas, teniendo presente que el Sol contiene 109,05 diámetros terrestres y en él pueden meterse 1.301.200 Tierras.

Aristarco de Samos

En cuanto a los estudios de la distancia de la Luna, re cogido en su trabajo, que ciertamente es el único que ha llegado hasta nosotros, sobre las dimensiones del Sol y la Luna y de las distancias de estos a nuestro planeta, decir tiene que calculó la distancia a la Luna, por medio de un eclipse de Luna, donde la sombra de la Tierra, era proyectada sobre la primera. Según la curvatura que presentaba, dedujo la distancia.

A Aristarco, que procede de la Escuela Alejandrina, se le atribuye también el hecho de ser el primero en pensar que la Tierra gira alrededor del Sol, precursor pues de Nicolás Copérnico* Además concibió el movimiento de las mareas como perteneciente a hechos astronómicos.

No fue sin embargo hasta la puesta en escena del astrónomo griego Hiparco de Nicea Bitinia (194 a 120 a.C.) cuan do las distancias comenzaron a ser más precisas. Basándose en los cálculos obtenidos de Eratóstenes en cuanto al diámetro terrestre (12.800 Km.), concluyó con que la distancia Tierra - Luna tendría que ser igual a 30 diámetros terrestres; es decir, 380.000 Km., aceptándose hoy una distancia media de 384.317,2 Km., siendo la máxima de 406.610 Km. y mínima de 356.334 Km.

Hiparco de Nicea

El calculador Hiparco, es conocido al mismo tiempo por averiguar el ángulo de inclinación de la eclíptica, conocer con mucha precisión los eclipses (mejor los de Luna que los de Sol), pues había calculado y estudiado el movimiento sinódico, sideral, dracónico a anómalo de la Luna, que ya veremos más adelante. Confeccionó un catálogo de 1.080 estrellas que es el primer catálogo estelar conocido, dividiendo el brillo de las estrellas en seis escalas o magnitudes según fueran más o menos luminosas. Parece ser que el catálogo fue realizado a raíz de la aparición de una nova o supernova en la constelación de Escorpión en el año 134 a.C. Dicho catálogo no ha llegado hasta nuestras manos.

Se dio cuenta de que el punto equinoccial cambiaba de posición con los años. Podríamos seguir contando muchos más descubrimientos, pero solo diremos que fue el maestro de la Astronomía antigua, aun que eso sí, dentro de las limitaciones de la época también creía que la Tierra era centro del Universo, aunque esto no empobrece su curriculum en ningún aspecto.

Otra forma de conocer la distancia Tierra-Luna

Conociendo ya la distancia Tierra - Luna, no era muy laborioso saber su diámetro; el de la Luna. Ello dependía del diámetro aparente de la Luna que luce en el cielo, que viene a ser de 31' 05,2", esto arroja un resultado de 3.480 Km. de diámetro. Hoy se acepta para el radio lunar 1.738 Km., o 3.476 Km. de diámetro.

La Luna varía su diámetro mes a mes a lo largo de todo el año, pues continuamente se aleja y acerca a la Tierra al describir su órbita sobre el planeta madre. Cuando se localiza la Luna en el perigeo, que es el punto más cercano de su órbita con respecto a la Tierra, su diámetro aparente en el cielo, resulta ser de 33' 50" (diámetro aparente máximo), mientras que cuando se sitúa en el apogeo, o punto más alejado de la órbita lunar con respecto a la Tierra el diámetro mínimo de superficie proyectada en el cielo, es de 28' 22"

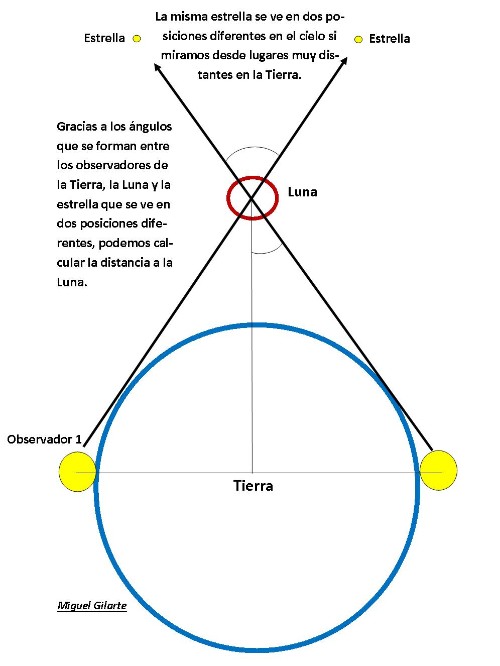
En cuanto a las estimaciones de la distancia a la Luna, hablaré rápidamente del método del paralaje, en el cual se utiliza la trigonometría sobre un triángulo imaginario y precisos instrumentos de observación (ver Fig. 1).

Supongamos que poseemos un amigo que vive en Barcelona, mientras los presentes, residimos en Sevilla. Separados de nuestro amigo por una distancia de 1.046 Km. Ambos poseemos un telescopio con aparatos de precisión para medir. Apuntamos ahora al unísono los telescopios hacia la Luna y tomamos su posición con respecto a las estrellas que se sitúan detrás de ella. Hemos formado un triángulo imaginario cuya base es la distancia entre Sevilla y Barcelona. Los dos ángulos de la base los conocemos, al trazar los lados del triángulo hacia las estrellas pasando por la Luna. Ahora solo tenemos que hacer cálculos trigonométricos precisos, para unir los lados del triángulo conocido y dibujar el nuevo ángulo donde se unen los lados.

La base del triángulo imaginario, también la podemos hallar por nuestra cuenta. Solo necesitamos del movimiento de rotación de la Tierra que ya existe. Este movimiento nos desplazará a lo largo de un tiempo (por ejemplo 12 horas) desde una posición a otra del espacio, trazando la línea mucho más amplia que la anterior que nos servirá como base.

Pero de todas formas estos métodos resultan anticuados y han quedado en desuso. Se ha impuesto la moderna -técnica, el avance científico y la era de los viajes espaciales. Así pues, los cálculos más precisos con error máximo de pocos centímetros, que se obtienen del cálculo de la distancia de la Luna, se toman gracias al espejo reflector que se instaló en ella, concretamente en el Mare Tranquilitatis (Mar de la Tranquilidad) durante la misión del Apolo XI el 26 de Julio de 1969.

La medición de la distancia, se obtiene lanzando desde la Tierra un rayo láser hacia el espejo que mira a nuestro planeta; conociendo la velocidad de desplazamiento del rayo (velocidad luz y el tiempo que emplea en toparse con el espejo y regresar a casa, se deduce con extrema precisión, la distancia Tierra - Luna. Gracias a este moderno ensayo, se ha llegado a averiguar como la Luna se aproxima a la Tierra a una lentitud pasmosa, que la hará chocar contra la Tierra teóricamente, puesto que el impacto tendrá lugar dentro de más de 45.000.000.000 de años, pero mucho antes, (40.000 millonea de años antes del contacto) el Sol habrá acabado de agotar su combustible y se expansionará quemando a todo el Sistema Solar.

Asociación Astronómica de España